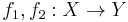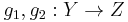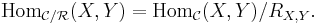Quotient category

In mathematics, a quotient category is a category obtained from another one by identifying sets of morphisms. The notion is similar to that of a quotient group or quotient space, but in the categorical setting.

1 Definition
2 Properties
3 Examples
4 See also
5 References

Definition

Let C be a category. A congruence relation R on C is given by: for each pair of objects X, Y in C, an equivalence relation R_X,Y on Hom(X,Y), such that the equivalence relations respect composition of morphisms. That is, if

$f_1,f_2�: X \to Y\,$

are related in Hom(X, Y) and

$g_1,g_2�: Y \to Z\,$

are related in Hom(Y, Z) then g₁f₁ and g₂f₂ are related in Hom(X, Z).

Given a congruence relation R on C we can define the quotient category C/R as the category whose objects are those of C and whose morphisms are equivalence classes of morphisms in C. That is,

$\mathrm{Hom}_{\mathcal C/\mathcal R}(X,Y) = \mathrm{Hom}_{\mathcal C}(X,Y)/R_{X,Y}.$

Composition of morphisms in C/R is well-defined since R is a congruence relation.

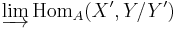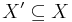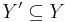There is also a notion of taking the quotient of an Abelian category A by a Serre subcategory B. This is done as follows. The objects of A/B are the objects of A. Given two objects X and Y of A, we define the set of morphisms from X to Y in A/B to be $\varinjlim \mathrm{Hom}_A(X', Y/Y')$ where the limit is over subobjects $X' \subseteq X$ and $Y' \subseteq Y$ such that 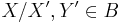$X/X', Y' \in B$ . Then A/B is an Abelian category, and there is a canonical functor 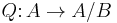$Q \colon A \to A/B$ . This Abelian quotient satisfies the universal property that if C is any other Abelian category, and 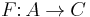$F \colon A \to C$ is an exact functor such that F(b) is a zero object of C for each 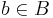$b \in B$ , then there is a unique exact functor 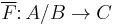$\overline{F} \colon A/B \to C$ such that 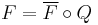$F = \overline{F} \circ Q$ . (See [Gabriel].)

Properties

There is a natural quotient functor from C to C/R which sends each morphism to its equivalence class. This functor is bijective on objects and surjective on Hom-sets (i.e. it is a full functor).

Examples

Monoids and group may be regarded as categories with one object. In this case the quotient category coincides with the notion of a quotient monoid or a quotient group.
The homotopy category of topological spaces hTop is a quotient category of Top, the category of topological spaces. The equivalence classes of morphisms are homotopy classes of continuous maps.

References

Gabriel, Pierre, Des categories abeliennes, Bull. Soc. Math. France 90 (1962), 323-448.
Mac Lane, Saunders (1998) Categories for the Working Mathematician. 2nd ed. (Graduate Texts in Mathematics 5). Springer-Verlag.

Quotient category

Contents

Definition

Properties

Examples

See also

References